0 引言

　　數控機床伺服進給系統是按誤差控制的系統，傳統的方法是采用PID控制。常規PID控制原理簡單，容易實現，穩態無靜差，因此長期以來廣泛應用于工業過程控制，并取得了良好的控制效果。然而，傳統的PID控制主要是控制具有確定模型的線性過程，而實際上，伺服系統運行情況復雜，具有參數時變性和模型不確定性，而且進給系統動態特性的模型建立涉及到摩擦特性的分析，同時還須考慮擾動扭矩的因素，尤其是機械系統的阻尼、剛度慣量等參數，要獲得較好的PID參數很困難。模糊控制理論是控制領域中非常有發展前途的一個分支，它以不依賴于被控對象的數學模型而被廣泛的應用于工業生產中。模糊控制具有較強的魯棒性、對被控對象的參數變化不敏感，超調量小等優點。本文將模糊控制與傳統PID控制相結合應用于數控機床的伺服控制系統中，同時針對控制對象具有非線性、時變性、隨機性等特點，構造了自適應模糊控制器，在控制過程中實時自動調整模糊控制參數，并對其進行仿真取得了良好的控制效果。

1 數控機床進給伺服系統控制模型的建立

　　數控機床通常由數控系統、伺服電機、位置或速度傳感器及工作臺等組成。CNC用來存儲工件加工程序、與計算機通訊、進行各種插補，向各個軸伺服驅動器發出控制命今。伺服電機接收CNC的控制命令后，快速、平滑的驅動工作臺運動。傳感器完成速度反饋實現閉環控制。系統組成如圖1所示。

圖1數控機床交流伺服系統

　　在以光柵、脈沖編碼器等組成檢測反饋環節所實現的閉環控制下，電動機的轉角將跟隨數控指令變化。通過高精度的齒輪副和精密絲杠螺母副傳動，電動機的角位移被轉化為所需的工作臺的直線位移。把機械部分和電氣部分連接組成數控機床位置伺服系統如圖2所示。由于機械傳遞環節對系統的影響，顯然，如果仍然采用常規PID整定方法調節參數無法滿足伺服系統的動態性能要求。由圖2可知，在較為全面考慮伺服系統的各個組成部分的特性后，系統傳遞函數是一個帶滯后環節的五階系統，為了研究方便，將其轉化為欠阻尼的二階系統。

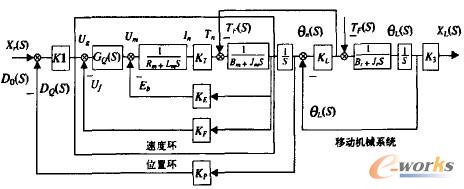
圖2伺服進給系統控制結構圖

2 自適應模糊PID控制器的設計

　　2.1 自適應模糊PID控制器的系統結構

　　模糊自適應PID控制系統的結構如圖3所示。由圖可見該系統由常規PID控制和模糊推理控制兩部分組成，以偏差e和偏差變化率e_c作為模糊控制器的輸入，根據模糊控制規則對PID參數進行自適應調整，以滿足不同e和ec時對控制參數的要求。

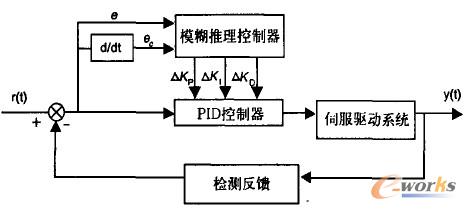
圖3模糊自適應PID控制系統的結構原理 

　　2.2 模糊控制器的結構

　　在MATLAB的命令窗口中輸入fuzzy，出現FIS editor的界而，即可在此方便地編輯所需的模糊推理系統。選擇控制器類型為Mamdani型，取And(與)的方法為min，Or(或)的方法為max，Implication(推理)的方法為min，Aggregation(合成)的方法為max，Defuzzification(去模糊化)的方法為centroid(重心平均法)。由圖3可看出該模糊控制器有兩輸入(e、e_c)，三輸出(△K_p、△K_i、△K_d)，打開FIS editor的下拉菜單edit，在Add Variable中選定輸入輸出變量數目。

　　2.2.1 隸屬度函數

　　設輸入輸出變量均選用三角形隸屬度函數曲線，論域為[6，+6]，模糊子集為{負大，負中，負小，零，正小，正中，正大}，分別對應{NB，NM，NS，0，PS，PM，PB}。雙擊各輸入輸出變量圖標，打開membership function editor(隸屬度函數編輯器)即可分別進行上述設定。

　　2.2.2 模糊控制規則

　　通常，PID控制器的控制算式為：

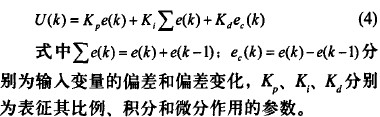
　　比例系數K_p的作用在于加快系統的響應速度，提高系統調節精度，K_p越大，響應速度越快，調節精度越高，但過大將產生超調，甚至導致系統不穩定。積分系數K_i的作用在于消除系統穩態誤差，K_i越大，靜差消除越快，但過大會產生積分飽和而引起較大的超調。微分系數K_d影響系統的動態特性，K_d越大，越能抑制偏差變化，但過大會延長調節時問，降低抗干擾能力。

　　根據參數K_p、K_i、K_d對系統輸出特性的影響情況，可歸納出系統在被控過程中對于不同的e和e_c，參數K_p、K_i、K_d的自整定原則：

　　1)當｜e｜ 較小時，為使系統具有較好的跟蹤性能，應取較大的K與較小的巧，同時為避免系統響應出現較大的超調，應對積分作用加以限制，通常取K_i=0。

　　2)當｜e｜和｜e_c｜為中等大小時，為使系統響應的超調量減小和保證一定的響應速度，Kp應取小一些。在這種情況下巧的取值對系統影響很大，應取小一些，Ki的取值要適當。

　　3)當｜e｜較小時，為了使系統具有較好的穩態性能，應增大K_p、K_i值，同時為避免輸出響應在設定值附近振蕩，以及考慮系統的抗干擾能力，應適當選取髟，其原則是：當偏差變化率較小時，K_p取大一些；當偏差變化率較大時，K_d取較小的值，通常K_d為中等大小。

　　由上述分析可得出模糊控制規則表，在edit下的Rules即可輸入模糊控制規則，形如：

　　至此，建立起名為nh．fis的文件，完成了模糊控制器結構的整體設計。

　　2.3 建立Fuzzy-PID系統結構仿真框圖

　　根據常規的PID控制器增量算式結合(1)、(2)、(3)式，即可在MATLAB／Simulink環境下建立起PID的仿真子模塊，如圖4所示，并封裝成子系統PIDSubsystem。模糊控制器及其封裝仿真模塊如圖5所示。把模糊控制器和PID控制器封裝在一起，組成Fuzzy—PID控制器，如圖6所示。

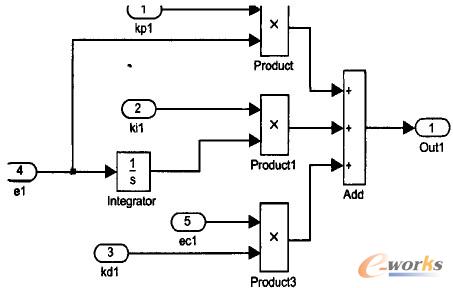
圖4 PID仿真子模塊

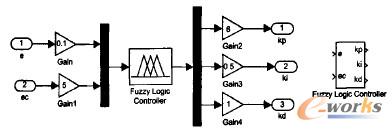
圖5模糊控制器及其封裝 

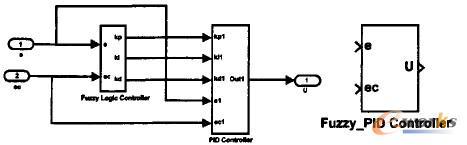
圖6模糊自適應PID控制器及其封裝 

3 系統仿真

　　選擇某數控機床的z向進給伺服系統為研究對象，工作臺質量m=3500kg，絲杠導程L=0.0012m，絲杠總長l=0.963m，絲杠支承軸向剛度KB=1.12*108N／m，絲杠螺母的接觸剛度KN=2.02*108N／m。采用西門子電機型號為IFKl602，電機轉動慣量J=0.01323kg·m²。根據以上參數確定機電耦合系統的傳遞函數，建立系統的模糊自適應PID控制的Simulink仿真計算圖，如圖7所示。

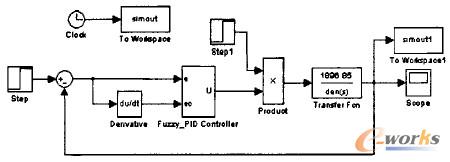
圖7系統模糊自適應PID控制的Simulink仿真 

　　取量化因子k_e=0.2，k_ec=0.1，解模糊因子k₁=0.5，k₂=0.01，k₃=0.01，令PID控制器3個初始值K_p'=16.4，K_i'=0.3，K_d'=0.5，仿真時間40s，加單位階躍信號圖6是常規PID控制曲線圖和模糊自適應PID控制曲線圖。仿真結果表明，此方法較常規的PID控制，由于模糊控制器能夠根據系統誤差e和e．誤差變化率對三個參數△K_p、△K_i、△K_d進行在線修正，所以得到的系統動態響應曲線較好，超調量小，穩態精度高，更好的適應性和魯棒性。

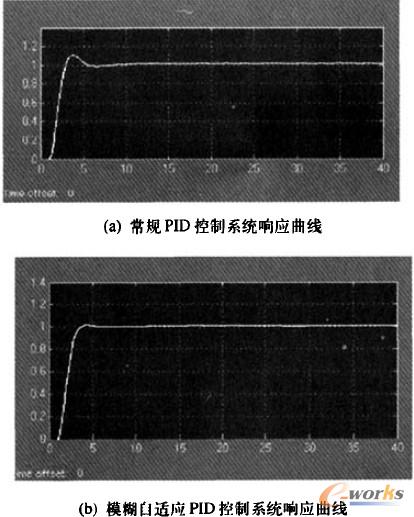
圖8控制性能比較

4 結論

　　本文介紹了基于模糊控制的伺服控制系統的基本結構，并詳細分析了各組成部分的機理，在此基礎上，將模糊PID控制應用于考慮機電耦合效應(包括機械進給環節)的數控伺服系統中，該控制器可以根據測量得到的偏差及偏差的變化率，在線自動整定PID控制器的3個參數，并在MATLAB環境下進行了仿真，仿真及實驗結果表明，自適應模糊位置控制器具有良好的穩態精度和動態響應。 

核心關注：拓步ERP系統平臺是覆蓋了眾多的業務領域、行業應用，蘊涵了豐富的ERP管理思想，集成了ERP軟件業務管理理念，功能涉及供應鏈、成本、制造、CRM、HR等眾多業務領域的管理，全面涵蓋了企業關注ERP管理系統的核心領域，是眾多中小企業信息化建設首選的ERP管理軟件信賴品牌。

轉載請注明出處：拓步ERP資訊網http://m.vmgcyvh.cn/

本文標題：模糊自適應PID在數控進給伺服系統的應用

本文網址：http://m.vmgcyvh.cn/html/consultation/1083939957.html