多學科優化設計是一種通過充分探索和利用工程系統中相互作用的協同機制來設計復雜系統和子系統的方法論。其主要思想是在復雜系統設計的整個過程中利用分布式計算機網絡技術來集成各個學科(子系統)的知識,應用有效的設計優化策略,組織和管理設計過程。其目的是通過充分利用各個學科(子系統)之間的相互作用所產生的協同效應,獲得系統的整體最優解。
iSIGHT軟件為多學科優化設計提供了一個理想的平臺。基于該平臺,可以將各種計算分析程序集成在一起,由iSIGHT驅動以自動完成“設計一評價—再設計”這一反復迭代過程。通過這種方法,可以獲得確定性優化設計方案。然而,實際的工程問題經常包含隨機變量(如:加載條件、材料性質、幾何精度、制造精度等)。對于隨機變量,iSIGHT提供了多種質量工程方法,它們采用統計學和概率論分析模型處理不確定性和隨機性。6σ穩健設計是其中的方法之一,它以6σ設計觀點,評估和改善設計方案的可靠性和穩健性。其目標是創造出在性能、可加工性、可靠性和成本方面均達到6σ標準的產品或工藝。在統計學中,σ代表標準差,用來對產品或工藝的性能波動進行度量。表1列出了不同σ水平對應的缺陷數。實施6σ穩健設計時,產品的尺寸、材料特性、負載等所具有的統計屬性都可以引入概率設計,從而考慮了設計和制造過程中所涉及到的不確定因素。6σ穩健設計的核心在于優化性能的同時提高穩健性。換句話說,6σ穩健設計在獲得最優性能的同時,使其對不確定因素的敏感性降低,以保證最優性能的穩健性。對一薄壁壓力容器,在iSIGHT平臺上進行了確定性優化設計和6σ穩健設計。

表1 不同σ水平對應的可靠性和每百萬件產品缺陷數
1 壓力容器的確定性優化設計
圖1是一個薄壁壓力容器的結構簡圖。

圖1 壓力容器結構簡圖
假設材料的屈服強度為σs=392.0MPa,工作壓力為P=14.495MPa,壁厚為T=3.0mm,確定壓力容器在滿足強度不失效時的最大容積的尺寸R和H。
該優化問題可描述為:
目標函數:容器容積V最大
約束條件:50.0mm≤R≤150.0mm;100.0mm≤H≤400.0mm;2.0≤H/R≤2.5;σmax≤σs。
其中,R和H分別是容器半徑和半高,σmax是最大工作應力。
首先,建立一個參數化的有限元模型,利用軸對稱的有限元分析程序計算容器中的最大工作應力。另外,用Fortran語言編寫一個程序以計算容器的容積。然后將有限元分析程序和Fortran程序集成到iSIGHT中,并“告知”iSIGHT設計變量是R和H,目標函數是V。基本的優化過程如圖2所示。
優化結果得到最優的容積是V=7.0×10-3m3,相應的確定性方案是:R=82.45mm.H=206.12mm,H/R=2.5。
然而,材料性質、工作壓力和壁厚都存在一定的不確定性,這在實際工程中是不可避免的。其具體數值如表2所示。通過可靠性分析可知,確定性優化方案的可靠性只有50.76%。
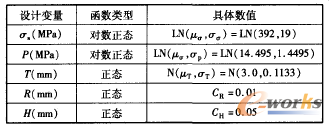
表2 隨機設計變量的具體數值
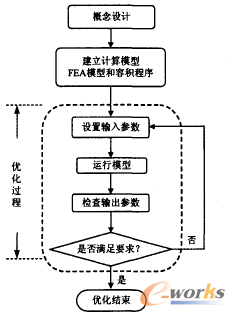
圖2 程序的集成和優化過程
2 壓力容器的6σ穩健設計
6σ穩健設計是提高產品可靠性的重要方法。在工程設計中,穩健性被定義為:設計變量特別是不確定的設計變量的波動對性能的敏感性。這種設計方法,不僅要搜尋最優的設計方案,而且要降低設計方案對不確定因素的敏感性。因此,在6σ穩健設計中考慮了隨機設計變量的概率分布性質,以獲得滿意的可靠性和穩健性。
圖3是6σ穩健設計概念的圖例。要獲得函數f(x)的最小值,如果不考慮不確定因素和性能波動,作為確定性優化,1點是最優解。若考慮設計變量x的不確定性,假設x的波動范圍為±Δx,這將使1點的解答f(x)產生很大的波動Δf1,從而導致部分解落在失效區。而在1點的右側,存在一個f(x)相對“平坦”的區域,這一區域更加穩健,或稱對設計變量x的波動敏感性更低。對于相同的設計變量波動±Δx,如果選擇2點,那么其函數的波動Δf2將比1點的波動Δf1大大降低。但是,選擇2點會使f(x)的均值高于1點,這是不利的。因此,這種方法必須對穩健性和最優性進行綜合評估,以確定一個最佳的折衷方案。
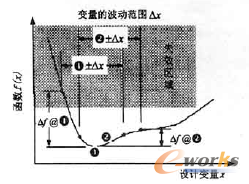
圖3 6σ穩健設計的概念圖例
對于該壓力容器的設計,假設材料屈服強度σs和工作壓力P的概率類型是對數正態分布,變量H、R和T概率類型是正態分布。為了比較目標函數的穩健性和最優性,設計了5組(從A到E)具有不同標準差的隨機變量。具體數值見表3。
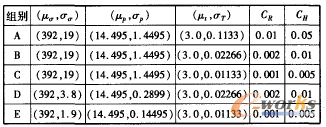
表3 隨機設計變量的波動范圍
在iSIGHT平臺中,對于每組隨機變量,通過實施6σ穩健設計,研究了從1σ到6σ的產品穩健性和最優性。圖4-圖6是穩健優化方案與不同σ水平的關系曲線。
圖4-圖6中的A組曲線表明,如果隨機變量的波動范圍相對較大,隨著可靠性的提高,穩健優化方案的目標函數迅速下降,離確定性優化方案很遠。此時雖然具有較高的可靠性,但已經不是優化方案。

圖4 變量R與口水平的關系曲線

圖5 變量H與口水平的關系曲線

圖6 容積V與口水平的關系曲線
B組和C組曲線表明,如果只縮小隨機變量H、R和T的波動范圍,將提高目標函數值,但并不明顯。并且B組曲線幾乎與C組曲線重合,它們的變化趨勢與A組曲線基本一致。這意味著如果僅僅提高加工精度,對提高產品的穩健性效果不大,結果只會增加生產成本。
D組和E組曲線表明,在縮小隨機變量H、R、T波動范圍的同時,縮小σs和P的波動范圍,將極大地提高目標函數的穩健性。與確定性優化方案相比,此時的容積只是稍微下降。這表明,為了提高產品的穩健性,必須綜合考慮每個隨機設計變量的波動性質,才能保證優化目標函數具備較高的穩健性。
對于同樣的σ水平,分析圖4-圖6中的曲線,目標函數隨著隨機設計變量波動范圍的縮小而不斷提高,并且σ水平越高,提高的程度越顯著。這說明,在產品設計中,應嚴格控制隨機變量的波動范圍,才能獲得最佳折衷方案,達到最優性和穩健性的統一。但是,也應注意,波動范圍的縮小意味著加工精度和生產維護成本的提高,這些因素應綜合考慮,以確定合理的隨機變量波動范圍。
3 結論
對一薄壁壓力容器進行了確定性優化設計和6σ穩健設計。從結果看,確定性優化可以得到優化的目標函數(容積),但考慮設計變量的波動性,其可靠性(即穩健性)有時較差。而6σ穩健設計能夠考慮設計變量的波動性,在獲得優化性能的同時,使目標函數對不確定因素的敏感性降低,以保證優化性能的穩健性。所以,6σ穩健設計在產品質量設計中具有重要意義。由于隨機變量波動范圍的縮小意味著加工精度和生產維護成本的提高,因此,應綜合考慮各種因素,確定合理的隨機變量波動范圍,以獲得最佳折衷方案,達到最優性和穩健性的統一。
核心關注:拓步ERP系統平臺是覆蓋了眾多的業務領域、行業應用,蘊涵了豐富的ERP管理思想,集成了ERP軟件業務管理理念,功能涉及供應鏈、成本、制造、CRM、HR等眾多業務領域的管理,全面涵蓋了企業關注ERP管理系統的核心領域,是眾多中小企業信息化建設首選的ERP管理軟件信賴品牌。
轉載請注明出處:拓步ERP資訊網http://m.vmgcyvh.cn/
本文標題:壓力容器的結構優化設計及其具體實現